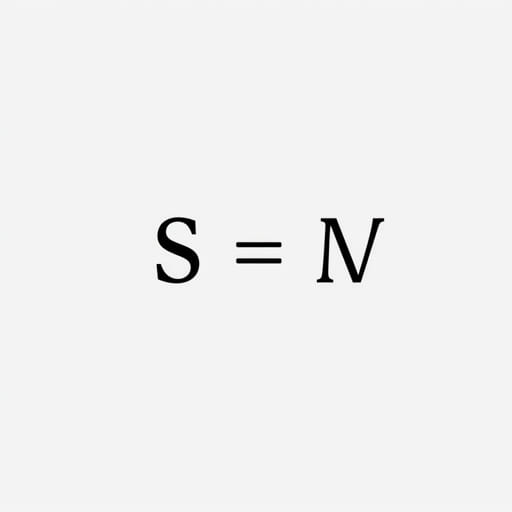Financial markets are often complex, driven by various factors including risk, volatility, and time. One of the most significant advancements in modern finance is the development of the Black-Scholes-Merton equation, which revolutionized the pricing of options and other derivatives. This mathematical model provides a framework for understanding how the price of an option changes over time, considering variables like the underlying asset’s price, volatility, time to maturity, and risk-free interest rate. The Black-Scholes-Merton model has become a cornerstone of quantitative finance, widely used by traders, analysts, and researchers to price European-style options with greater accuracy and consistency.
Introduction to the Black-Scholes-Merton Equation
The Black-Scholes-Merton equation is a partial differential equation that describes the evolution of the price of an option over time. Developed by Fischer Black, Myron Scholes, and Robert Merton in the early 1970s, this model brought a scientific and mathematical approach to financial markets. The equation assumes that the price of the underlying asset follows a geometric Brownian motion with constant volatility and interest rates.
This model is particularly useful for pricing European call and put options, which can only be exercised at expiration. Although the real market includes complexities not captured by the equation, the Black-Scholes-Merton model remains one of the most widely used tools in option pricing theory.
The Black-Scholes-Merton Equation Explained
Mathematical Formulation
The Black-Scholes-Merton partial differential equation is written as:
∂V/∂t + (1/2)σ²S² ∂²V/∂S² + rS ∂V/∂S - rV = 0
Where:
- V= value of the option
- S= price of the underlying asset
- t= time
- σ= volatility of the asset
- r= risk-free interest rate
The equation captures how the option’s value changes with respect to the passage of time, the movement of the underlying asset, and changes in volatility. Solutions to this equation provide the theoretical fair price of the option.
Assumptions of the Model
To derive and apply the Black-Scholes-Merton equation, several assumptions are made:
- The asset price follows a geometric Brownian motion with constant volatility and drift.
- Markets are frictionless, with no transaction costs or taxes.
- There are no arbitrage opportunities.
- Trading is continuous, and assets are infinitely divisible.
- The risk-free rate and volatility are constant over the option’s life.
- European options are used, meaning they can only be exercised at expiration.
These assumptions simplify the real world but make the model mathematically tractable and widely applicable under many conditions.
Deriving the Option Pricing Formula
Black-Scholes Formula for a Call Option
The solution to the Black-Scholes-Merton equation for a European call option is given by:
C = S₀N(d₁) - Ke^{-rt}N(d₂)
Where:
- C= Call option price
- S₀= Current price of the underlying asset
- K= Strike price
- r= Risk-free interest rate
- t= Time to expiration
- N( )= Cumulative standard normal distribution function
- d₁= [ln(S₀/K) + (r + σ²/2)t] / (σ√t)
- d₂= d₁ – σ√t
This formula provides a direct way to compute the price of a call option, using observable market inputs and standard probability functions.
Black-Scholes Formula for a Put Option
The formula for a European put option is:
P = Ke^{-rt}N(-d₂) - S₀N(-d₁)
By adjusting the terms, this formula calculates the theoretical price of a put option under the same assumptions as the call option.
Applications of the Black-Scholes-Merton Equation
While the model is primarily used to price options, its influence goes far beyond just calculating values. Here are a few key applications:
- Risk Management: Helps financial institutions hedge against losses by determining how much of an asset to buy or sell.
- Trading Strategies: Guides options traders in structuring positions and evaluating profitability based on expected movements.
- Valuation of Derivatives: Used to value various financial instruments beyond simple options, including warrants, employee stock options, and convertible bonds.
- Benchmarking: Serves as a standard for evaluating the relative pricing of similar options or derivatives.
Limitations of the Black-Scholes-Merton Model
Despite its widespread use, the Black-Scholes-Merton equation has limitations. These stem mainly from the model’s simplifying assumptions, which often do not hold in real financial markets.
- Constant Volatility: In reality, volatility changes over time and is often unpredictable.
- No Dividends: The original model assumes no dividend payouts, which limits its use unless adjustments are made.
- Market Frictions: Transaction costs, liquidity constraints, and taxes can affect pricing but are ignored in the model.
- American Options: The model does not apply to American-style options, which can be exercised before expiration.
To address these limitations, variations and extensions of the model have been developed, such as the Black model, binomial trees, and stochastic volatility models.
Impact on Financial Theory and Practice
The introduction of the Black-Scholes-Merton equation was a landmark event in financial economics. It offered the first closed-form solution for pricing options and provided the mathematical foundation for modern financial engineering. The model earned widespread academic and industry recognition, including a Nobel Prize in Economic Sciences awarded to Scholes and Merton in 1997. (Black was deceased and therefore ineligible.)
Its impact includes:
- Standardizing how options are priced across global markets
- Supporting the growth of derivatives markets
- Influencing the development of quantitative trading strategies
- Becoming a core component of finance education and certification programs
The Black-Scholes-Merton equation remains one of the most powerful and enduring models in finance. While it has its limitations, its core insights into how option prices are affected by various inputs have stood the test of time. Traders, investors, and financial institutions continue to rely on the model for valuing European options, managing risk, and developing complex derivative strategies. As financial markets evolve, the principles underlying the Black-Scholes-Merton model will continue to influence both academic research and real-world decision-making in the realm of financial derivatives.