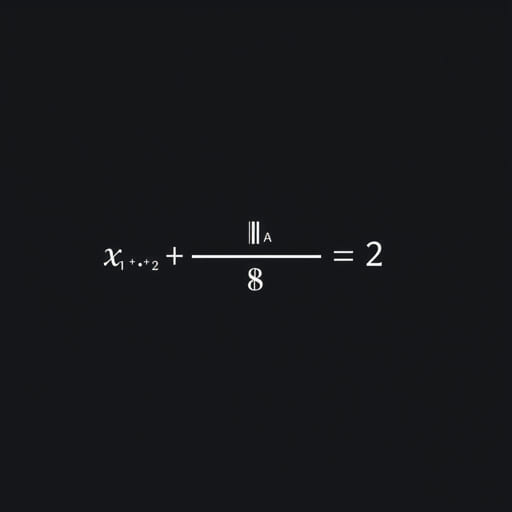How To Solve Nonlinear Differential Equations

August 15, 2025 Admin

How to Solve Nonlinear Differential Equations A Comprehensive GuideNonlinear differential equations arise in a wide variety of applications, from modeling physical systems to understanding complex phenomena in biology, chemistry, and engineering. Unlike linear differential equations, which can often be solved with straightforward methods, nonlinear differential equations require more advanced techniques. This topic will guide you through the methods used to solve nonlinear differential equations, presenting them in a simple and easy-to-understand manner.

Table of Contents

What Are Nonlinear Differential Equations?

Nonlinear differential equations are equations in which the unknown function and its derivatives appear to a power greater than one or are involved in non-linear operations such as multiplication or division. These equations are often more challenging to solve compared to linear differential equations due to their complexity and the lack of straightforward solutions.

For example, a simple nonlinear differential equation might look like this

frac{dy}{dx} = y^2 – x

Here, the equation involves a non-linear term y^2 , making it nonlinear. Unlike linear equations, which have solutions that form straight lines, solutions to nonlinear equations can exhibit more complex behavior, such as oscillations or chaotic systems.

Methods to Solve Nonlinear Differential Equations

Solving nonlinear differential equations typically involves several approaches depending on the form of the equation. While some nonlinear differential equations can be solved analytically, many others require numerical methods. Below are some of the most commonly used methods for solving nonlinear differential equations.

1. Separation of Variables

Separation of variables is a technique that can be used when the nonlinear differential equation can be written in the form

frac{dy}{dx} = g(x)h(y)

In this form, the variables x and y are separable, meaning the equation can be rearranged so that all terms involving x are on one side and all terms involving y are on the other side.

For example, consider the equation

frac{dy}{dx} = y^2 – x

We can rewrite this as

frac{dy}{y^2 – x} = dx

At this point, we integrate both sides to find the solution. The key idea is to separate the variables x and y so that each side can be independently integrated.

2. Substitution Methods

In some cases, nonlinear differential equations can be simplified by making an appropriate substitution. The substitution is often chosen to reduce the degree of nonlinearity or to transform the equation into a more solvable form.

For example, consider the following nonlinear differential equation

frac{dy}{dx} = y^2 + 2y

We can simplify this by introducing a substitution such as v = y + 1 , turning the equation into a simpler form. Substituting and simplifying often transforms the equation into one that is easier to handle, allowing you to solve it more effectively.

3. Using Linearization

Linearization is a technique used to approximate the solution to a nonlinear differential equation by approximating it as a linear equation near a specific point, often around equilibrium points. This method is particularly useful for understanding the behavior of nonlinear systems near steady states.

For example, if you have a nonlinear differential equation like

frac{dy}{dx} = y^3 – 2y

You can linearize this equation around a point by finding the derivative of the right-hand side with respect to y at that point. This results in a linear approximation that can be solved using standard methods.

4. Homogeneous Equations

Many nonlinear differential equations are homogeneous, meaning that they can be written as

Fleft( frac{dy}{dx}, y, x right) = 0

For these types of equations, it is possible to reduce the order of the equation by making a suitable substitution. The substitution typically takes the form of v = frac{y}{x} , and this allows the equation to be transformed into a separable form, making it easier to solve.

5. Numerical Methods

In cases where an analytical solution is difficult or impossible to find, numerical methods are used to approximate the solution. One of the most common numerical techniques is the Euler method, which is used for solving ordinary differential equations. More advanced numerical methods include Runge-Kutta methods and Finite Difference methods.

Numerical methods provide a way to obtain an approximate solution at discrete points. These methods are particularly useful for complex nonlinear equations that do not have closed-form solutions.

Example Solving a Nonlinear Differential Equation

Let’s walk through an example of how to solve a nonlinear differential equation using the separation of variables method.

Consider the nonlinear equation

frac{dy}{dx} = frac{y}{x^2}

Step 1 Separate Variables

First, we separate the variables

frac{dy}{y} = frac{dx}{x^2}

Step 2 Integrate Both Sides

Now, we integrate both sides of the equation

int frac{1}{y} , dy = int frac{1}{x^2} , dx

The integrals are

ln |y| = -frac{1}{x} + C

Where C is the constant of integration.

Step 3 Solve for y

Finally, we solve for y

y = e^{-frac{1}{x} + C}

This is the general solution to the differential equation.

Challenges in Solving Nonlinear Differential Equations

Solving nonlinear differential equations can be challenging because

Complex Solutions Nonlinear equations often have solutions that are difficult to express in a closed form. The solutions can be oscillatory, chaotic, or involve multiple branches.
Lack of General Methods Unlike linear equations, where methods such as the characteristic equation or Laplace transforms provide general solutions, nonlinear equations often require case-specific approaches.
Numerical Approximation In many cases, nonlinear differential equations cannot be solved exactly, and numerical methods must be used, which can introduce errors and require computational resources.

Solving nonlinear differential equations is a critical skill for mathematicians, scientists, and engineers alike. The complexity of these equations requires a range of techniques, from substitution and linearization to numerical methods for approximating solutions. While some nonlinear differential equations can be solved using elementary methods, many others require more advanced techniques, especially in cases where an analytical solution is not possible. With practice and a solid understanding of the available methods, solving nonlinear differential equations becomes more manageable and rewarding.

Understanding the principles outlined in this guide will help you approach these types of equations with confidence, whether you are working in academia, research, or industry.